
Back Функцие тишкерни CV Curve sketching English Étude de fonction French वक्र का अनुरेखण Hindi Penggambaran kurva ID Perbincangan graf Malay Przebieg zmienności funkcji Polish Trasarea graficului unei curbe Romanian Исследование функции Russian Дослідження функції Ukrainian

−1 < x < 5,
0 < y < 12
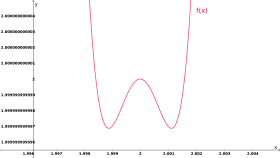
1,995 < x < 2,005,
1,999999999995 < y < 2,000000000005
Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen geometrische Eigenschaften, wie zum Beispiel Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte, Wendepunkte, gegebenenfalls Sattel- und Flachpunkte, Asymptoten, Verhalten im Unendlichen usw. Diese Informationen erlauben es, eine Skizze des Graphen anzufertigen, aus der all diese für die Funktion charakteristischen Eigenschaften unmittelbar ablesbar sind.
Es ist heute hingegen nicht mehr das Ziel einer Kurvendiskussion, den Menschen dabei zu unterstützen, eine möglichst genaue Zeichnung des Graphen der Funktion zu produzieren: das kann inzwischen jeder Funktionsplotter (etwa ein grafikfähiger Taschenrechner, ein Smartphone mit entsprechender Software, ein Tabellenkalkulationsprogramm oder Computeralgebra-Software) besser.
Ziel der Kurvendiskussion ist vielmehr,
- die Koordinaten der charakteristischen Punkte des Graphen exakt zu bestimmen (aus einem Funktionsplot lassen sich lediglich ungefähre Werte ablesen);
- charakteristische Eigenschaften wie Symmetrie oder Verhalten im Unendlichen zu beweisen. Aus einem Funktionsplot kann man immer nur Aussagen über den abgebildeten Ausschnitt des Koordinatensystems ablesen, z. B. für den Bereich , . Ob der Graph einer Funktion aber z. B. bei noch einmal einen „Schlenker“ macht oder nicht, darüber kann nur auf der Grundlage einer Kurvendiskussion eine zuverlässige Aussage getroffen werden.
- genauer hinzusehen: ein augenscheinliches globales Minimum kann sich – bei entsprechender Vergrößerung – als ein lokales Maximum herausstellen. Man vergleiche etwa die beiden Plots der Funktion
- in Abbildung 1 bzw. Abbildung 2. Eine Kurvendiskussion deckt solche Phänomene stets auf, ob sie sich im Molekülbereich oder in astronomischen Dimensionen abspielen: weil eine Kurvendiskussion nicht – wie ein Funktionsplot – von der Auflösung abhängt.
Zudem lässt sich eine Kurvendiskussion auch ganz ähnlich bei Funktionen durchführen, die von vielen Variablen abhängen (also z. B. von , und anstelle von nur ). Eine zwei- oder dreidimensionale Visualisierung einer derartigen Funktion ist nicht mehr möglich.
Die Bedeutung der Kurvendiskussion wird auch deutlich vor dem Hintergrund, dass in entscheidungsunterstützenden Systemen Hoch- bzw. Tiefpunkte automatisch, d. h. ohne Benutzerinteraktion, zu berechnen sind. Soll beispielsweise die Auswirkung der Veränderung einer Randbedingung auf die zu optimierende Größe untersucht werden, so würde solch ein System den jeweiligen Extremwert anzeigen bzw. grafisch visualisieren, während ein Wert, der die Randbedingung beschreibt (etwa die Höhe einer Ressource), variiert wird.







