Back ላፕላስ ሽግግር Amharic تحويل لابلاس Arabic Tresformada de Laplace AST Преобразование на Лаплас Bulgarian লাপ্লাস রূপান্তর Bengali/Bangla Laplaceova transformacija BS Transformada de Laplace Catalan Laplaceova transformace Czech Laplacetransformation Danish Μετασχηματισμός Λαπλάς Greek
Die Laplace-Transformation, benannt nach Pierre-Simon Laplace, ist eine einseitige Integraltransformation, die eine gegebene Funktion vom reellen Zeitbereich in eine Funktion im komplexen Spektralbereich (Frequenzbereich; Bildbereich) überführt. Diese Funktion wird Laplace-Transformierte oder Spektralfunktion genannt.
Die Laplace-Transformation hat Gemeinsamkeiten mit der Fourier-Transformation, vermeidet aber die dort auftretenden Konvergenzprobleme bei nicht absolut integrierbaren, aber praktisch wichtigen Signalen.
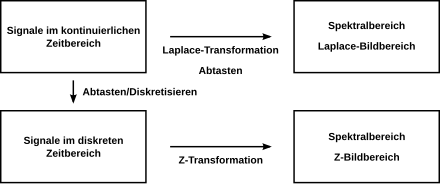
Sie ist auf kausale Signale mit kontinuierlichem Zeitbereich anwendbar und verwandt mit der Z-Transformation, einer entsprechenden Transformation für Signale mit diskretem Zeitbereich.