
Back رباعي الأبعاد Arabic Polychor Czech Polychor German Plurĉelo Esperanto Polícoro Spanish 4-polytope French Policoro (matematica) Italian 多胞体 Japanese 4차원 다포체 Korean Polychoron Dutch
| {3,3,3} | {3,3,4} | {4,3,3} |
|---|---|---|
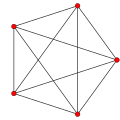 5-cell Pentatope 4-simplex |
 16-cell Orthoplex 4-orthoplex |
 8-cell Tesseract 4-cube |
| {3,4,3} | {3,3,5} | {5,3,3} |
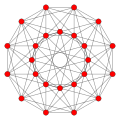 24-cell Octaplex |
 600-cell Tetraplex |
 120-cell Dodecaplex |
In geometry, a 4-polytope (sometimes also called a polychoron,[1] polycell, or polyhedroid) is a four-dimensional polytope.[2][3] It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.[4]
The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron.
Topologically 4-polytopes are closely related to the uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be cut and unfolded as nets in 3-space.
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.1 Polytopes and Honeycombs, p.224
- ^ Vialar, T. (2009). Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance. Springer. p. 674. ISBN 978-3-540-85977-2.
- ^ Capecchi, V.; Contucci, P.; Buscema, M.; D'Amore, B. (2010). Applications of Mathematics in Models, Artificial Neural Networks and Arts. Springer. p. 598. doi:10.1007/978-90-481-8581-8. ISBN 978-90-481-8580-1.
- ^ Coxeter 1973, p. 141, §7-x. Historical remarks.