Bounded function

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Bounded function" – news · newspapers · books · scholar · JSTOR (September 2021) (Learn how and when to remove this message)

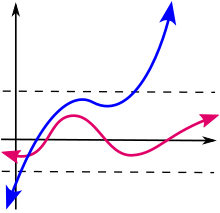
In mathematics, a function ${\displaystyle f}$ defined on some set ${\displaystyle X}$ with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number ${\displaystyle M}$ such that

${\displaystyle |f(x)|\leq M}$

for all ${\displaystyle x}$ in ${\displaystyle X}$.^[1] A function that is not bounded is said to be unbounded.^{[citation needed]}

If ${\displaystyle f}$ is real-valued and ${\displaystyle f(x)\leq A}$ for all ${\displaystyle x}$ in ${\displaystyle X}$, then the function is said to be bounded (from) above by ${\displaystyle A}$. If ${\displaystyle f(x)\geq B}$ for all ${\displaystyle x}$ in ${\displaystyle X}$, then the function is said to be bounded (from) below by ${\displaystyle B}$. A real-valued function is bounded if and only if it is bounded from above and below.^{[1][additional citation(s) needed]}

An important special case is a bounded sequence, where ${\displaystyle X}$ is taken to be the set ${\displaystyle \mathbb {N} }$ of natural numbers. Thus a sequence ${\displaystyle f=(a_{0},a_{1},a_{2},\ldots )}$ is bounded if there exists a real number ${\displaystyle M}$ such that

${\displaystyle |a_{n}|\leq M}$

for every natural number ${\displaystyle n}$. The set of all bounded sequences forms the sequence space ${\displaystyle l^{\infty }}$.^{[citation needed]}

The definition of boundedness can be generalized to functions ${\displaystyle f:X\rightarrow Y}$ taking values in a more general space ${\displaystyle Y}$ by requiring that the image ${\displaystyle f(X)}$ is a bounded set in ${\displaystyle Y}$.^{[citation needed]}