
Back بيان موجه خال من الحلقات Arabic Graf acíclic dirigit Catalan Rettet acyklisk graf Danish Graph (Graphentheorie)#Teilgraphen.2C Wege und Zyklen German Κατευθυνόμενος άκυκλος γράφος Greek Grafo acíclico dirigido Spanish گراف جهتدار غیرمدور Persian Suunnattu syklitön verkko Finnish Graphe orienté acyclique French גרף מכוון חסר מעגלים HE
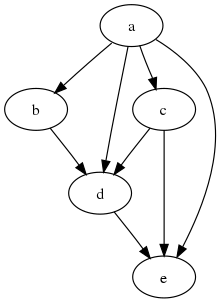
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called arcs), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling).
Directed acyclic graphs are also called acyclic directed graphs[1] or acyclic digraphs.[2]