Hooke's law

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2017) (Learn how and when to remove this message)

Part of a series on
Continuum mechanics
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Fick's laws of diffusion
Laws Conservations Mass Momentum Energy Inequalities Clausius–Duhem (entropy)
Solid mechanics Deformation Elasticity linear Plasticity Hooke's law Stress Strain Finite strain Infinitesimal strain Compatibility Bending Contact mechanics frictional Material failure theory Fracture mechanics
Fluid mechanics Fluids Statics · Dynamics Archimedes' principle · Bernoulli's principle Navier–Stokes equations Poiseuille equation · Pascal's law Viscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure Liquids Adhesion Capillary action Chromatography Cohesion (chemistry) Surface tension Gases Atmosphere Boyle's law Charles's law Combined gas law Fick's law Gay-Lussac's law Graham's law Plasma
Rheology Viscoelasticity Rheometry Rheometer Smart fluids Electrorheological Magnetorheological Ferrofluids
Scientists Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t e

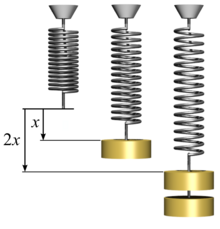
In physics, Hooke's law is an empirical law which states that the force (F) needed to extend or compress a spring by some distance (x) scales linearly with respect to that distance—that is, F_s = kx, where k is a constant factor characteristic of the spring (i.e., its stiffness), and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram.^[1][2] He published the solution of his anagram in 1678^[3] as: ut tensio, sic vis ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660.

Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean.

Hooke's law is only a first-order linear approximation to the real response of springs and other elastic bodies to applied forces. It must eventually fail once the forces exceed some limit, since no material can be compressed beyond a certain minimum size, or stretched beyond a maximum size, without some permanent deformation or change of state. Many materials will noticeably deviate from Hooke's law well before those elastic limits are reached.

On the other hand, Hooke's law is an accurate approximation for most solid bodies, as long as the forces and deformations are small enough. For this reason, Hooke's law is extensively used in all branches of science and engineering, and is the foundation of many disciplines such as seismology, molecular mechanics and acoustics. It is also the fundamental principle behind the spring scale, the manometer, the galvanometer, and the balance wheel of the mechanical clock.

The modern theory of elasticity generalizes Hooke's law to say that the strain (deformation) of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the "proportionality factor" may no longer be just a single real number, but rather a linear map (a tensor) that can be represented by a matrix of real numbers.

In this general form, Hooke's law makes it possible to deduce the relation between strain and stress for complex objects in terms of intrinsic properties of the materials they are made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness k directly proportional to its cross-section area and inversely proportional to its length.