Simpson's rule

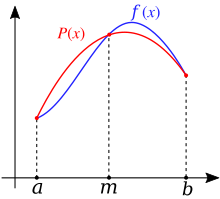
In numerical integration, Simpson's rules are several approximations for definite integrals, named after Thomas Simpson (1710–1761).

The most basic of these rules, called Simpson's 1/3 rule, or just Simpson's rule, reads $${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right].}$$

In German and some other languages, it is named after Johannes Kepler, who derived it in 1615 after seeing it used for wine barrels (barrel rule, Keplersche Fassregel). The approximate equality in the rule becomes exact if f is a polynomial up to and including 3rd degree.

If the 1/3 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson's 1/3 rule. Points inside the integration range are given alternating weights 4/3 and 2/3.

Simpson's 3/8 rule, also called Simpson's second rule, requires one more function evaluation inside the integration range and gives lower error bounds, but does not improve on order of the error.

If the 3/8 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson's 3/8 rule.

Simpson's 1/3 and 3/8 rules are two special cases of closed Newton–Cotes formulas.

In naval architecture and ship stability estimation, there also exists Simpson's third rule, which has no special importance in general numerical analysis, see Simpson's rules (ship stability).