Back مسألة جسمين Arabic Problema de los dos cuerpos AST Задача двух цел Byelorussian Задача с две тела Bulgarian Problema dels dos cossos Catalan Икĕ ĕскер тĕллевчĕкĕ CV Zweikörperproblem German Problema de los dos cuerpos Spanish Kahe keha probleem Estonian Bi gorputzen arazo Basque
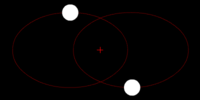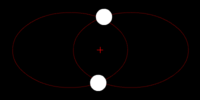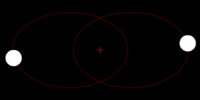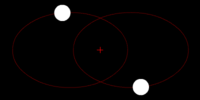
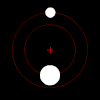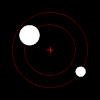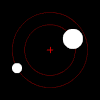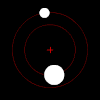
Right: Two bodies with a "slight" difference in mass orbiting a common barycenter. Their sizes and this type of orbit are similar to the Pluto–Charon system (in which the barycenter is external to both bodies), as well as the Earth–Moon system (in which the barycenter is internal to the larger body).
| Part of a series on |
| Astrodynamics |
|---|
In classical mechanics, the two-body problem is to calculate and predict the motion of two massive bodies that are orbiting each other in space. The problem assumes that the two bodies are point particles that interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored.
The most prominent example of the classical two-body problem is the gravitational case (see also Kepler problem), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as satellites, planets, and stars. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions.
A simpler "one body" model, the "central-force problem", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (as with a light planet orbiting a heavy star, where the star can be treated as essentially stationary).
However, the one-body approximation is usually unnecessary except as a stepping stone. For many forces, including gravitational ones, the general version of the two-body problem can be reduced to a pair of one-body problems, allowing it to be solved completely, and giving a solution simple enough to be used effectively.
By contrast, the three-body problem (and, more generally, the n-body problem for n ≥ 3) cannot be solved in terms of first integrals, except in special cases.