Centra angulo

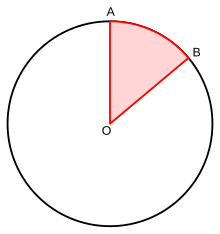
En cirklo, centra angulo estas angulo kies apekso (vertico) estas en la centro de la cirklo kaj kies du flankoj estas du radiusoj de cirklo. La grando de la angulo en radianoj egalas al la longo de la arko, kiun ĉi tiu angulo intersekcas de cirklo kies radiuso egalas 1. La grando de la centra angulo Θ estas 0° < Θ < 360 ° (notita en gradoj) aŭ 0 < Θ < 2π radianoj.

Laŭ difino de centra angulo, kiu ripozas sur punktoj A kaj B, kiuj estas sur la cirklo, oni devas determini ĉu ĉi tiu estas la konveksa angulo ( < 180 °) aŭ la konkava > 180 °). Ĉi tiuj du anguloj estas egalaj laŭ grando kiam la centra angulo estas 180 ° (kaj la centra angulo estas fakte diametro).

Kiam la malgranda arko limigita inter la flankoj de la centra angulo estas L, la radiuso de la cirklo estas R, la cirkonferenco de la cirklo estas 2πR kaj la arko L estas la parto ${\displaystyle {\frac {\Theta }{2\pi }}}$ De la tuto, do:

${\displaystyle L={\frac {\Theta }{2\pi }}\cdot 2\pi R\,\Rightarrow \,\Theta ={\frac {L}{R}}}$

Fakto: Kiam la tanĝanto al la cirklo ĉe punkto A kaj la tanĝanto al la cirklo ĉe punkto B renkontiĝas ĉe punkto P ekster la cirklo, tiam ∠BOA (konveksa) kaj ∠BPA kompletigas unu la alian ĝis 180 °.

Fakto: La grandeco de la ĉirkaŭa angulo, kiu ripozas sur la sama arko, sur kiu ripozas la centra angulo, egalas al duono de la grandeco de la centra angulo.

La flankoj de la centra angulo kaj la arko barita inter ili formas sektoron. La proporcio inter la areo de la sektoro kaj la tuta areo de la cirklo egalas al la proporcio inter la centra angulo kaj kompleta rotacio, kaj egala al la proporcio inter la arka longo de la sektoro kaj la cirkonferenco de la tuta rondo. Tio signifas ke la areo de la sektoro estas: ${\displaystyle S={\frac {\theta \cdot r^{2}}{2}}={\frac {L\cdot r}{2}}}$ kiam ${\displaystyle L}$ estas la longo de la arko kaj la anguloj estas mezuritaj per radianoj.