Okedro

Okedro
Plia nomo	Triangula kontraŭprismo
Klaku por rigardi turnantan bildon
Speco	Regula pluredro Trianguledra pluredro
Vertica figuro	3.3.3.3
Bildo de vertico
Bildo de reto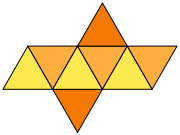
Simbolo de Wythoff	4 | 2 3
Simbolo de Schläfli	{3,4} kaj ${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}}$
Figuro de Coxeter-Dynkin
Indeksoj	U05 C17 W2
Simbolo de Bowers	Oct
Verticoj	6
Lateroj	12
Edroj	8
Edroj detale	8{3}
χ	2
Geometria simetria grupo	Oh
Duedra angulo	arccos(-1/3) ~= 109,47122°
Duala	Kubo
Bildo de duala
v • d • r

Okedro estas pluredro kun 8 edroj. La regula okedro estas platona solido komponita el de 8 egallateraj trianguloj. En ĉiu vertico kuniĝas 4 edroj.

La okedra geometria simetria grupo estas O_h de ordo 48. Subgrupoj de ĉi tiu grupo estas D_3d (ordo 12), la geometria simetria grupo de triangula kontraŭprismo; D_4h (ordo 16), la geometria simetria grupo de kvadrata dupiramido; T_d (ordo 24), la geometria simetria grupo de rektigita kvaredro. Ĉi tiuj simetrioj povas esti emfazitaj per malsamaj dekoracioj de la edroj.

Ĝi estas tri-dimensia kruca hiperpluredro. Ĝi estas ankaŭ triangula kontraŭprismo.

La regula okedro havas 6 verticojn kaj 12 randojn, ĉi tio estas la minimumo inter diversaj okedro; neregulaj okedroj povas havi 12 verticojn kaj 18 randojn.^[1]

Estas kvar grava specoj de okedroj kun duedra simetrio:

• Seslatera prismo: 6 kvadratoj, 2 seslateroj
• Seplatera piramido: 7 trianguloj, 1 seplatero
• Kvarlatera dupiramido: 8 trianguloj, kutime izocelaj, en ĉi tiun specon trafas la regula okedro se la trianguloj estas egallateraj.
• Kvarlatera trapezoedro - 8 deltoidoj

La vorto okedro estas malofte uzata en ĉi tiu ĝenerala senco ĉar ĉi tiuj pluredroj ne havas gravajn komunajn propraĵoj.

1. ↑ Arkivita kopio. Arkivita el la originalo je 2011-10-10. Alirita 2007-06-27.