
Back Parallaks Afrikaans اختلاف المنظر Arabic Paralax AST Parallaks Azerbaijani Паралакс Byelorussian Паралякса BE-X-OLD Паралакс Bulgarian Paralaks BJN লম্বন Bengali/Bangla Paral·laxi Catalan
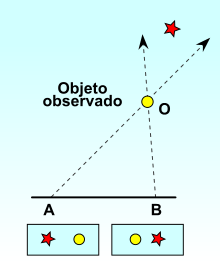
Al proyectar el objeto observado O contra un fondo suficientemente distante, la posición de O varía según el punto de vista en A o en B. Desde A, el objeto observado parece estar a la derecha de la lejana estrella roja, mientras que desde B se ve a la izquierda de aquella.
El ángulo AOB se denomina ángulo de paralaje, que abarca el segmento AB desde O.
El paralaje (del griego παράλλαξις [parálaksis], ‘cambio’, ‘diferencia’) es la desviación angular de la posición aparente de un objeto, dependiendo del punto de vista elegido.[1]
Debido al acortamiento, los objetos cercanos muestran un paralaje mayor que los objetos lejanos, por lo que el paralaje puede utilizarse para determinar distancias.
Para medir grandes distancias, como la distancia de un planeta o una estrella a la Tierra, los astrónomos utilizan el principio de paralaje. En este caso, el término paralaje es el semiángulo de inclinación entre dos líneas de visión de la estrella, como se observa cuando la Tierra está en lados opuestos del Sol en su órbita.[2] Estas distancias forman el peldaño más bajo de lo que se denomina "la escalera de distancias cósmicas", el primero de una sucesión de métodos por los que los astrónomos determinan las distancias a los objetos celestes, sirviendo de base para otras mediciones de distancias en astronomía que forman los peldaños superiores de la escalera.
El paralaje también afecta a instrumentos ópticos como visores, binoculares, microscopios y cámara réflex de objetivos gemelos que ven objetos desde ángulos ligeramente diferentes. Muchos animales, junto con los humanos, tienen dos ojos con campos visuales superpuestos que utilizan el paralaje para obtener percepción de profundidad; este proceso se conoce como estereopsis. En visión por ordenador el efecto se utiliza para la visión estereoscópica por ordenador, y existe un dispositivo llamado telémetro de paralaje que lo utiliza para encontrar la distancia, y en algunas variaciones también la altitud a un objetivo.
Un sencillo ejemplo cotidiano de paralaje puede verse en los salpicaderos de los vehículos de motor que utilizan un velocímetro mecánico de aguja. Cuando se mira directamente desde delante, la velocidad puede ser exactamente 60, pero cuando se mira desde el asiento del pasajero, la aguja puede parecer que muestra una velocidad ligeramente diferente debido al ángulo de visión combinado con el desplazamiento de la aguja desde el plano de la esfera numérica.
- ↑ Buscador urgente de dudas: «Paralaje es la traducción de parallax», artículo publicado el 11 de abril de 2018 en el sitio web Fundéu BBVA (Madrid), asesorado por la Real Academia Española.
Todas las palabras terminadas con «aje» tienen género masculino, excepto paralaje, que aparece en el diccionario de la RAE con ambos géneros:- el alunizaje
- el anclaje
- el andamiaje
- el antidopaje
- el aprendizaje
- el arbitraje
- el aterrizaje
- el bricolaje
- el cabotaje
- el camuflaje
- el caudillaje
- el cronometraje
- el desembalaje
- el doblaje
- el embalaje
- el encaje
- el ensamblaje
- el equipaje
- el espionaje
- el espionaje
- el follaje
- el fuselaje
- el kilometraje
- el largometraje
- el lenguaje
- el libertinaje
- el maquillaje
- el masaje
- el millaje
- el montaje
- el mueblaje
- el oleaje
- el patrullaje
- el peaje
- el pelaje
- el peregrinaje
- el personaje
- el pillaje
- el porcentaje
- el rastrillaje
- el reciclaje
- el reglaje
- el relaje
- el reportaje
- el taquillaje
- el tonelaje
- el tutelaje
- el vasallaje
- el villaje
- ↑ En el pasado paralaje diurno también se utilizaba para medir distancias a objetos celestes dentro del sistema solar. Este método ha sido sustituido por técnicas más precisas.