Pi (zenbakia)

«Pi» orriak hona dakar. Bestelako esanahiei buruzko orria hau da: «Pi (argipena)»

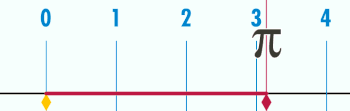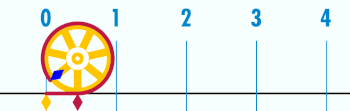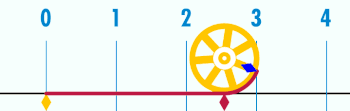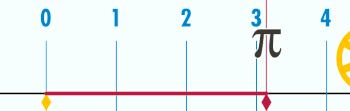
${\displaystyle \pi }$ zenbakia (pi ahoskatua) konstante matematiko bat da. Originalki zirkulu baten zirkunferentzia eta bere diametroaren arteko harreman gisa adierazten zen, baina gaur egun hainbat definizio pareko ditu, eta formula anitzetan agertzen da matematika eta fisikako esparru guztietan. Gutxi gora behera 3,14159 balio du. ${\displaystyle \pi }$ greziar letra erabili izan da XVIII. mendearen ondotik.

Zenbaki irrazional bat izanda, ${\displaystyle \pi }$ ezin da adierazi zatiki baten moduan. ${\displaystyle \pi }$ren errepresentazio dezimala ez da inoiz amaitzen eta ez du errepikatzen den patroirik. Hala ere, ${\displaystyle {22}/{7}}$ bezalako zatikiak eta beste zenbaki arrazional batzuk erabili izan dira ${\displaystyle \pi }$ zenbakira hurbildu ahal izateko. Ematen duenez, dezimaletako zenbakiak ausaz daude banatuak. Uste da ${\displaystyle \pi }$ zenbakiaren digituen sekuentziak ausazko banaketa estatistiko mota bat dela, baina gaur egun ez da honen inguruko froga zehatzik lortu. ${\displaystyle \pi }$ zenbaki transzendental bat da; hau da, ez da koefiziente arrazionalak dituen zero-ez-den polinomio baten erroan dagoen zenbaki bat. ${\displaystyle \pi }$ren transzendentzia honek esan nahi du ezinezkoa dela antzinarotik hedatu izan den zirkuluaren koadratura ebaztea erregela eta konpasa erabilita.

Antzinaroko zibilizazioek arrazoi praktikoak direla eta ${\displaystyle \pi }$ren balio nahiko zehatzak behar zituzten. Antzinako Egiptoko eta Babiloniako matematikan jada egin ziren kalkulu nahiko zehatzak. K.a. 250.urtearen inguruan Arkimedes greziar matematikariak algoritmo bat sortu zuen ${\displaystyle \pi }$ kalkulatu ahal izateko. Txinako matematikariek zazpi digituko gerturapena eskuratu zuten, metodo geometrikoak bakarrik erabilita, eta bost digituko gerturapena Indiako matematikariek V. mendean. Serie infinitutan oinarritutako ${\displaystyle \pi }$ren lehen formula historiko zehatza milurteko bat beranduago aurkitu zen, Indiako matematikariek Madhava–Leibniz seriea aurkitu zutenean^[1][2]. XX. eta XXI. mendean matematikariek eta informatikariek gerturapen berriak asmatu zituzten, eta ordenagailuen boterearen handitzearekin, ${\displaystyle \pi }$ren errepresentazio dezimala hainbat bilioi digituraino zabaldu zen^[3]. Aplikazio zientifiko ia guztiek ez dute behar ${\displaystyle \pi }$ren ehun digitu baino gehiago behar eta askok askoz gutxiago, beraz gaur egungo dezimalen bilaketa honen helburu nagusia algoritmo hobeak aurkitzea da, eta errekor berriak hausteko nahia^[4][5]. Kalkulu estentsibo horiek superordenadoreak eta algoritmoen biderketen prezisio altua frogatzeko erabiltzen dira.

Bereziki zirkuluei lotuta definitzen delako, trigonometria eta geometriako formula askotan agertzen da, bereziki zirkulu, elipse eta esferekin lotuta daudenak. Analisi matematiko modernoan, zenbaki errealen sistemaren ezaugarri espektralak erabiltzen definitzen da, periodo baten autobalio gisa, geometriari erreferentziarik egin gabe. Horregatik, matematikako eta zientzietako hainbat eremutan agertzen da, geometria eta zirkuluekin harremanik izan gabe ere; zenbakien teorian eta estatistikan eta fisikako eremu ia guztietan agertzen da ${\displaystyle \pi }$. Nonahikotasun honek ${\displaystyle \pi }$ konstante matematiko ezagunetako bat izatea dakar, komunitate zientifikoaren barruan zein kanpoan. Zenbakiari dedikatutako liburu asko argitaratu dira, Pi Eguna ospatzen da eta ${\displaystyle \pi }$ren digitu berriak kalkulatzen direnean albiste izan ohi da. ${\displaystyle \pi }$ren balioa memorizatzeko lehiaketak egiten dira, eta gaur egun errekorra 70.000 digitutan ezarria dago^[6].

1. ↑ 1938-, Andrews, George E.,. (1999). Special functions. Cambridge University Press ISBN 0521789885. PMC 852896189..
2. ↑ Gupta, R.C. "On the Remainder Term in the Madhava-Leibniz's series." Canita Bhdrati 14: 68-71, 1992.
3. ↑ «22.4 trillion digits of pi» www.pi2e.ch (Noiz kontsultatua: 2018-03-06).
4. ↑ 1964-, Arndt, Jörg,. (2001). Pi-unleashed. Springer ISBN 9783540665724. PMC 45394279..
5. ↑ (Ingelesez) Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M.. (1997-12-01). «The quest for PI» The Mathematical Intelligencer 19 (1): 50–56.  doi:10.1007/BF03024340. ISSN 0343-6993. (Noiz kontsultatua: 2018-03-06).
6. ↑ (Ingelesez) «Most Pi places memorised» Guinness World Records (Noiz kontsultatua: 2018-03-06).
7. ↑ «JOSE RAMON ETXEBARRIA, INGENIARIA, IRAKASLEA ETA IDAZLEA “Pentsatzeko gaitasuna lortu duen materiamultzo bat gara”» eu.wikisource.org (Noiz kontsultatua: 2021-03-05).
8. ↑ Zapiain, Markos. (2020-02-05). «“Pentsatzeko gaitasuna lortu duen materiamultzo bat gara” JOSE RAMON ETXEBARRIA, INGENIARIA, IRAKASLEA ETA IDAZLEA» www.noticiasdegipuzkoa.eus (Noiz kontsultatua: 2021-03-04).