Zirkuluaren koadratura

Zirkulua koadratu: irudiko karratuaren eta zirkuluaren azaleren balioa π da. 1882an frogatu zen irudi hori ezin dela urrats kopuru finitu batean lortu, konpasa eta erregela erabiliz.

Denbora luzean, itxurazko soluzio partzial batzuek itxaropen faltsuak eman zituzten. Irudi honetan, ilundutako figura lunula da. Haren azalera ABC triangeluaren azaleraren berdina da (Quios-eko Hipocrates-ek emandako emaitza).

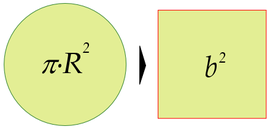
Zirkulua koadratzea antzinako matematikako hiru problema klasikoetako bat da. Problema geometriko hau, erregela eta konpasa bakarrik erabiliz, zirkulu baten azalera bera duen karratu bat lortzean datza. Problema geometriko hau eta zirkunferentzia bat zuzenki bihurtzea problema baliokideak dira. Bi problema hauek, era berean, π zenbakiaren eraikuntzarekin daude lotuta, unitate bateko luzera duen zuzenki batetik abiatuta.

π balioaren eraikuntza hau antzinako geometrek planteatu zuten, eta matematikariak  XIX. mendera arte saiatu ziren soluzioa aurkitzen, harik eta 1882an Carl Louis Ferdinand von Lindemann-ek ataza ezinezkoa zela frogatu zuen arte.

Matematikari honek frogatu zuen π balioa zenbaki transzendentea dela; eta ez aljebraikoa.  Bestela esanda, ez da koefiziente arrazionalak dituen polinomio baten erroa.

Zirkuluaren koadratura matematikako problemarik ezagunenetako bat da. Mendeetan zehar, matematikari profesional eta zaleek irtenbide bat bilatu zuten alferrik. Gaur egun, zirkulua koadratze kontzeptua metafora bihurtu da hizkuntza askotan, soluzio gabeko lan bat adierazteko^[1].

1. ↑ Abad Nebot, Francisco. (2001-01-01). [http://dx.doi.org/10.5944/epos.17.2001.10203 «RESEÑA de : Real Academia Española. Diccionario de la lengua española : vigésima segunda edición. Madrid : Real Academia Española de la Lengua, 2001»] Epos : Revista de filología (17): 488.  doi:10.5944/epos.17.2001.10203. ISSN 2255-3495. (Noiz kontsultatua: 2023-11-29).