Ibridizzazione

L'ibridazione (o ibridizzazione^[1]) è un procedimento di combinazione matematica di un certo numero di orbitali atomici (orbitali s, p) di valenza di un atomo, aventi energie poco diverse, che permette di ottenere per quell'atomo altrettanti nuovi orbitali ibridi equivalenti (isoenergetici tra loro, finché possibile), coi lobi orientati lungo le direzioni dettate dalla combinazione matematica stessa. Questi nuovi orbitali ibridi potranno essere usati dall'atomo per formare legami con altri atomi. Verrà preferito l'uso di orbitali ibridi, rispetto a quello di orbitali atomici, se i legami con essi formati con altri atomi comporterà un guadagno di stabilità per la molecola (legami più forti).

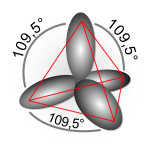
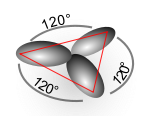
Il numero di orbitali ibridi ottenuti è uguale al numero di quelli che vengono combinati, cosicché il numero totale di orbitali di valenza dell'atomo non cambia. I lobi degli orbitali ibridi hanno nuove direzioni rispetto a quelli atomici e tali direzioni formano tra loro angoli caratteristici per ogni combinazione (sp, sp², sp³).

Il processo di ibridazione può essere accompagnato da un processo di promozione di uno o più elettroni in orbitali a livello energetico più alto allo scopo di ottenere un maggior numero di elettroni spaiati; questo ha un costo energetico che però può spesso (non sempre) essere più che compensato dal guadagno connesso con la formazione di un numero maggiore di legami e, come accennato sopra, legami più forti.

L'ibridazione consente di stabilire la forma geometrica di una molecola o di uno ione con il metodo di Gillespie (1957), che è un affinamento della teoria già elaborata nel 1940 da Nevil Sidgwick e Herbert Marcus Powell.

Le ibridazioni degli orbitali s e p possono essere di tipo:

• sp (dà luogo a due orbitali ibridi e strutture lineari);^[2] esempi di ibridazione sp si hanno nelle molecole di azoto (N₂), monossido di carbonio (CO), acetilene (C₂H₂), e fluoruro di berillio (BeF₂);
• sp² (dà luogo a tre orbitali ibridi e strutture trigonali planari);^[3] esempi di ibridazione sp² si hanno nelle molecole di trifluoruro di boro (BF₃), triossido di zolfo (SO₃), diossido di zolfo (SO₂), etene (C₂H₄), benzene (C₆H₆) e grafene;
• sp³ (dà luogo a quattro orbitali ibridi e strutture tetraedriche).^[4] esempi di ibridazione sp³ si hanno nelle molecole di metano (CH₄), ammoniaca (NH₃), acqua (H₂O), acido perclorico (HClO₄), acido solforico (H₂SO₄) e acido fosforico (H₃PO₄).

Per molecole ipervalenti come ${\displaystyle {\ce {PCl5}}}$ o ${\displaystyle {\ce {SF6}}}$ il concetto di ibridazione non può essere esteso, ma si fa riferimento a modelli più complessi; infatti, non possiamo descrivere in termini di ibridazione il rimescolamento di orbitali d con orbitali s e p poiché la differenza di energia è troppo elevata.^[5]