Elliptisk kurva

En elliptisk kurva är mängden av punkter ${\displaystyle (x,y)}$ som löser en polynomekvation som har grad två i ${\displaystyle y}$ och grad tre i ${\displaystyle x}$. Denna ekvation skrivs vanligtvis på formen

${\displaystyle y^{2}=x^{3}+a_{1}x+a_{2}\quad a_{i}\in k,}$

där k är en kropp där den elliptiska kurvan är definierad, till exempel reella talen. Samtliga elliptiska kurvor kan skrivas på formen

${\displaystyle y^{2}+a_{1}xy+a_{2}y=x^{3}+a_{3}x^{2}+a_{4}x+a_{5}.}$

För att få ekvationen på den enkla formen överst kan man kvadratkomplettera vänsterledet (om karakteristiken av kroppen k är skild från 2), och då får man

${\displaystyle \left(y+{\frac {a_{1}x+a_{2}}{2}}\right)^{2}=x^{3}+a_{3}x^{2}+a_{4}x+a_{5}.}$

Variabelbytet

${\displaystyle Y=\left(y+{\frac {a_{1}x+a_{2}}{2}}\right)}$

ger

${\displaystyle Y^{2}=x^{3}+a_{3}x^{2}+a_{4}x+a_{5},}$

och för att man skall få en användbar elliptisk kurva (se nedan) får ekvationen inte ha multipla rötter. Med ytterligare ett variabelbyte (om karakteristiken av kroppen k även är skild från 3) kan man skriva ekvationen på formen

${\displaystyle y^{2}=x^{3}+a_{4}x+a_{5}.}$

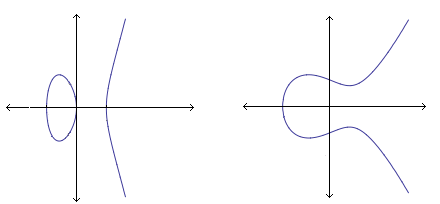
Grafen till denna funktion har två typer av huvudformer beroende på om ekvationen har en reell rot eller tre reella rötter. När ekvationen har tre reella rötter så består grafen av två komponenter, medan den bara har en komponent då ekvationen har en reell rot.

Elliptiska kurvor är inte direkt kopplade till ellipser, men namnet elliptiska kurvor kommer ifrån att de är besläktade med elliptiska integraler. Elliptiska integraler används för att beräkna båglängden på ellipser. En elliptisk integral kan se ut som följer:

${\displaystyle \int _{z_{1}}^{z_{2}}{\frac {dx}{\sqrt {x^{3}+bx+c}}}}$